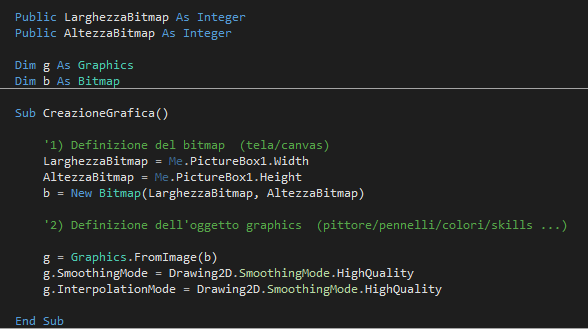
Generazioni di processi aleatori
I
linguaggi di programmazione ci permettono di generare e rappresentare
processi aleatori come ad esempio il moto browniano In questo articolo
vedremo e mostreremo come generare processi aleatori,
come ad esempio il moto browniano applicandoli all'ambito finanziario.
Il moto Browniano (Brownian motion)
Il moto browniano è sicuramente il più
importante tra i processi stocastici presi in esame. Il suo nome si deve
al lavoro del botanico R. Brown, è in realtà A. Einstein. Ricordiamo che
il moto Browniano standard è definito come un processo stocastico che parte
nell’origine, i cui incrementi sono indipendenti e distribuiti come una Normale
di media nulla e varianza pari all’ampiezza dell’incremento. Alcune proprietà
immediate sono la continuità e la non differenziabilità delle
traiettorie.
Se rappresentassimo il moto Browniano
standard unidimensionale noteremmo un’impressionante analogia con i
grafici di borsa e ciò non è un caso, esistono infatti molti risultati teorici
che collegano questo importante processo in tempo continuo all’evoluzione di
alcuni strumenti finanziari come le opzioni. Questo processo è spesso usato in
modelli finanziari per descrivere l'evoluzione dei prezzi nel tempo. Quando
viene applicato ai prezzi, il moto browniano presuppone che il passaggio da un
periodo all'altro non sono associati con il livello di prezzi oppure a serie
storiche delle variazioni dei prezzi e i processi dei prezzi sono indipendenti
e incorrelati. Cioè, ogni variazione di prezzo è indipendente dalle variazioni
di prezzo del passato e la volatilità delle variazioni dei prezzi è
costante.
Random Walk
Se sono fatti N realizzazioni, allora abbiamo una distribuzione binomiale:

Il fenomeno osservato, detto variabile, può essere osservato in dati istanti di tempo (variabile di stato: numero dei dipendenti di un'azienda, quotazione di chiusura di un titolo negoziato in borsa, livello di un tasso di interesse ecc.) o alla fine di periodi di lunghezza definita (variabili di flusso: vendite annuali di un'azienda, PIL trimestrale ecc.).
Indicando con Y il fenomeno, si indica con Yt un'osservazione al tempo t, potendo t variare da 1 a T, dove T è il numero complessivo degli intervalli o dei periodi temporali considerati.
In generale una serie storica è così definita yt={y1,y2,y3,....,yT};la serie storica avrà dimensione T.
FORMA BASE


La passeggiata
aleatoria, è il modello base utilizzato per descrivere i movimenti dei prezzi
azionari nei principali modelli di gestione del rischio. È una successione di
variabili aleatorie con uguale distribuzione di probabilità e indipendenti
l'una dall'altra.
Un esempio elementare di una
passeggiata aleatoria semplice è la distribuzione di Bernoulli che
assume il valore 1 con probabilità p ( un passo verso destra) e
-1 con probabilità 1 - p (un passo verso sinistra) ad
ogni passo. Un semplice, discreta, piedi unidimensionale
senza pregiudizi la stessa probabilità di andare a destra che a
sinistra, vale a dire  .
.
 .
.Se sono fatti N realizzazioni, allora abbiamo una distribuzione binomiale:
La distribuzione di probabilità è:

Serie storica
Si definisce come un insieme di variabili casuali
ordinate rispetto al tempo, ed esprime la dinamica di un certo fenomeno
nel tempo. Le serie storiche vengono studiate sia per interpretare un
fenomeno, individuando componenti di trend, di ciclicità, di stagionalità e/o di accidentalità, sia per prevedere il suo andamento futuro.
In generale, per serie
si intende la classificazione di diverse osservazioni di un fenomeno
rispetto ad un carattere qualitativo. Se tale carattere è il tempo, la
serie viene detta storica o temporale.Il fenomeno osservato, detto variabile, può essere osservato in dati istanti di tempo (variabile di stato: numero dei dipendenti di un'azienda, quotazione di chiusura di un titolo negoziato in borsa, livello di un tasso di interesse ecc.) o alla fine di periodi di lunghezza definita (variabili di flusso: vendite annuali di un'azienda, PIL trimestrale ecc.).
Indicando con Y il fenomeno, si indica con Yt un'osservazione al tempo t, potendo t variare da 1 a T, dove T è il numero complessivo degli intervalli o dei periodi temporali considerati.
In generale una serie storica è così definita yt={y1,y2,y3,....,yT};la serie storica avrà dimensione T.
Trasformazione di Box-Muller
È un metodo per generare coppie di numeri casuali indipendenti e distribuiti gaussianamente con media nulla e varianza uno.
La trasformazione viene comunemente espressa in due forme. La forma
principale è quella del lavoro originale: si campionano due numeri dalla
distribuzione uniforme sull'intervallo ![(0,1]](http://upload.wikimedia.org/math/6/6/8/668c7b55a37300c330dcd565d9e076da.png) e si ricavano due numeri distribuiti normalmente. La forma polare campiona due numeri su un intervallo differente (
e si ricavano due numeri distribuiti normalmente. La forma polare campiona due numeri su un intervallo differente (![[-1,+1]](http://upload.wikimedia.org/math/3/3/5/335c2d7c2ccfc1766a245197da8da7c8.png) ) e permette di ricavare due numeri distribuiti normalmente senza l'uso delle funzioni seno e coseno.
) e permette di ricavare due numeri distribuiti normalmente senza l'uso delle funzioni seno e coseno.
![(0,1]](http://upload.wikimedia.org/math/6/6/8/668c7b55a37300c330dcd565d9e076da.png) e si ricavano due numeri distribuiti normalmente. La forma polare campiona due numeri su un intervallo differente (
e si ricavano due numeri distribuiti normalmente. La forma polare campiona due numeri su un intervallo differente (![[-1,+1]](http://upload.wikimedia.org/math/3/3/5/335c2d7c2ccfc1766a245197da8da7c8.png) ) e permette di ricavare due numeri distribuiti normalmente senza l'uso delle funzioni seno e coseno.
) e permette di ricavare due numeri distribuiti normalmente senza l'uso delle funzioni seno e coseno.
Siano  e
e 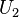 due variabili aleatorie indipendenti ed uniformemente distribuite nell'intervallo
due variabili aleatorie indipendenti ed uniformemente distribuite nell'intervallo ![(0,1]](http://upload.wikimedia.org/math/6/6/8/668c7b55a37300c330dcd565d9e076da.png) . Sia
. Sia
 e
e 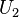 due variabili aleatorie indipendenti ed uniformemente distribuite nell'intervallo
due variabili aleatorie indipendenti ed uniformemente distribuite nell'intervallo ![(0,1]](http://upload.wikimedia.org/math/6/6/8/668c7b55a37300c330dcd565d9e076da.png) . Sia
. Sia
e

Allora Z0 e Z1 sono variabili aleatorie indipendenti con distribuzione normale di deviazione standard unitaria.
La dimostrazione è basata sul fatto che, in un sistema cartesiano
bidimensionale nel quale le coordinate X e Y sono descritte da due
variabili casuali indipendenti normalmente distribuite, le variabili
casuali R2 e  nelle corrispondenti coordinate polari sono a loro volta indipendenti e possono essere espresse come
nelle corrispondenti coordinate polari sono a loro volta indipendenti e possono essere espresse come e
e 
 nelle corrispondenti coordinate polari sono a loro volta indipendenti e possono essere espresse come
nelle corrispondenti coordinate polari sono a loro volta indipendenti e possono essere espresse come e
e