Calcolo del PNL su una lista di ordini

Il PNL o P/L profit/loss (utile/perdita) è un conto economico che offre informazioni inerenti la possibilità di ricavare profitti o perdite.  E' una dichiarazione di profitti e perdite anche noto come conto economico ed è anche una relazione che mostra i ricavi e le spese di una società in un determinato periodo di tempo, di solito un trimestre fiscale o un anno. E' anche uno delle tre dichiarazioni (oltre allo stato patrimoniale e rendiconto finanziario) più importanti nel processo di informativa finanziaria e si osserva l'utile netto di organizzazione o la perdita netta durante quel tempo.

L'utile netto è teoricamente a disposizione degli azionisti che possono decidere che anziché pagare i dividendi trattenere gli utili per futuri investimenti nel settore. L'utile netto è la fonte è la fonte di risarcimento per gli azionisti. Il PnL viene utilizzato per verificare l'ipotesi che i fattori di rischio identificati per una posizione rischiosa sono sufficienti a spiegare il cambiamento sostanziale dalla posizione rischiosa. Uno degli elementi più importanti di questo P & L è la linea di vendita, detta anche delle Entrate.

La 'linea di fondo' è quindi il risultato netto, in modo che il profitto che rimane dopo tutti i costi vengono sottratti. Per quanto riguarda l'immissione di un ordine nel mercato occorre selezionare il titolo solitamente attraverso la watchlist. Una watchlist è un elenco personalizzato di titoli periodicamente monitorati alla ricerca di occasioni di trading.

Il trader o l’investitore realizza queste liste sulla base di determinate caratteristiche utili al suo stile di trading. Nella watchlist si seleziona il titolo desiderato selezionando il titolo desiderato e cliccando su un apposito pulsante. All’interno di tale maschera devono essere inserite alcune informazioni obbligatorie e ne possono essere inserite altre opzionali.

Informazioni obbligatorie da inserire:

• Codice del titolo che si vuole negoziare: informazione solitamente precompilata in automatico grazie alla selezione del titolo di interesse sulla watchlist.

• Negoziazione che si vuole effettuare: identifica il verso della negoziazione(buy = acquisto o sell = vendita).

• Quantità che si vuole negoziare: quantità di titoli da acquistare o vendere.La quantità deve essere un multiplo del lotto minimo di negoziazione.

• Prezzo limite: permette di specificare, in caso di acquisto, il prezzo massimo che l’investitore è disposto a pagare, in caso di vendita il prezzo minimo al quale l’investitore è disposto ad alienare le attività finanziarie in oggetto.

• Periodo di validità dell’ordine: l’ordine può essere mantenuto valido sinoalla fine della giornata borsistica (dopo di che viene cancellato e deve essere eventualmente reinserito il giorno successivo), oppure può essere specificata una data fino alla quale l’ordine rimane sul mercato.

Siamo ora pronti per l’invio dell’ordine, che concretamente avviene premendo un tasto di “Invio ordine”.

Inoltre dopo aver svolto un ordine occorre valutare anche la commissione.
Una commissione è una tassa di servizio valutati da un broker o consulente di investimento in cambio di fornire consulenza sugli investimenti e / o la manipolazione l'acquisto o la vendita di un titolo. La maggior parte importante, società di intermediazione a servizio completo derivano la maggior parte dei loro profitti da commissioni di ricarica sulle transazioni dei clienti. Le commissioni variano notevolmente da intermediazione di intermediazione.

L'equazione di base su cui si basa il Pnl è:

PNL= PNL_Realized+PNL_unrealized

Il PNL_realized, invece, è dato dalla differenza tra il prezzo alla vendita e il prezzo all’acquisto, moltiplicata per la quantità venduta.

PNL_Realized = (Sell Price - Buy Price) * Qty

dove il Sell Price altro non è che la somma del prezzo d’entrata e del prezzo delle commissioni alla vendita mentre, in maniera analoga, il Buy Price è dato dalla somma tra il prezzo di entrata e il prezzo delle commissioni all’acquisto.

 

PNL_unrealized = (Theoretical Exit Price - Avg Price) * Position

•  Position =  posizione data dalla differenza del totale acquistato con il totale venduto.
• Theoretical Exit Price = prezzo teorico fissato a priori
•  Avg Price = prezzo medio, calcolato dividendo il costo (prezzo d’entrata + commissione)  per la posizione (questa quantità è fondamentale per calcolare il P&L unrealized).

Istogramma & Processo Aleatorio: Grafica & Interazione

In questo articolo in merito allo studio fatto in precedenza sui diversi processi aleatori applicati nell'ambito finanziario gli obiettivi preposti sono i seguenti: prima realizzeremo un istogramma all'interno della Picture Box , poi creeremo un rettangolo, contenuto nella Picture Box, in cui verrà posto l'istogramma e infine realizzeremo un programma in cui avremo sia un processo aleatorio che un istogramma al quale l'utente potrà modificare il numero di classi .

  

 Istogramma

 

 

L'output del codice è il seguente:

Premendo il tasto Button:

 Istogramma in un rettangolo

Mandando in esecuzione il programma con il tasto Avvia si ha il seguente Form:

Premendo il tasto Button si ottiene il seguente risultato:

 

Istogramma + Processo aleatorio
 

Mandando in esecuzione il programma si ottiene il seguente Form, in cui si può modificare il numero delle classi dell'istogramma accanto al bottone oppure lasciarlo inalterato.

 

Premendo il tasto Button si ottiene il seguente output:

Se cambiassi il numero di classi avrei:

 

Generazioni di processi aleatori

I linguaggi di programmazione ci permettono di generare e rappresentare processi aleatori come ad esempio il moto browniano In questo articolo vedremo e mostreremo come generare processi aleatori, come ad esempio il moto browniano applicandoli all'ambito finanziario.

Il moto Browniano (Brownian motion)

Il moto browniano è sicuramente il più importante tra i processi stocastici presi in esame. Il suo nome si deve al  lavoro del botanico R. Brown, è in realtà A. Einstein. Ricordiamo che il moto Browniano standard è definito come un processo stocastico che parte nell’origine, i cui incrementi sono indipendenti e distribuiti come una Normale di media nulla e varianza pari all’ampiezza dell’incremento. Alcune proprietà immediate sono la continuità e la non differenziabilità  delle traiettorie. 

Se rappresentassimo il moto Browniano standard unidimensionale noteremmo un’impressionante analogia con i grafici di borsa e ciò non è un caso, esistono infatti molti risultati teorici che collegano questo importante processo in tempo continuo all’evoluzione di alcuni strumenti finanziari come le opzioni. Questo processo è spesso usato in modelli finanziari per descrivere l'evoluzione dei prezzi nel tempo. Quando viene applicato ai prezzi, il moto browniano presuppone che il passaggio da un periodo all'altro non sono associati con il livello di prezzi oppure a serie storiche delle variazioni dei prezzi e i processi dei prezzi sono indipendenti e incorrelati. Cioè, ogni variazione di prezzo è indipendente dalle variazioni di prezzo del passato e la volatilità delle variazioni dei prezzi è costante. 

Random Walk

La passeggiata aleatoria, è il modello base utilizzato per descrivere i movimenti dei prezzi azionari nei principali modelli di gestione del rischio. È una successione di variabili aleatorie con uguale distribuzione di probabilità e indipendenti l'una dall'altra.

Un esempio elementare di una passeggiata aleatoria semplice è la  distribuzione di Bernoulli che assume il valore 1 con probabilità p ( un passo verso destra) e -1 con probabilità 1 - p (un passo verso sinistra) ad ogni passo. Un semplice, discreta, piedi unidimensionale senza pregiudizi la stessa probabilità di andare a destra che a sinistra, vale a dire  .

Se sono fatti N realizzazioni, allora abbiamo una distribuzione binomiale:

La distribuzione di probabilità è:

 

Serie storica 

Si definisce come un insieme di variabili casuali ordinate rispetto al tempo, ed esprime la dinamica di un certo fenomeno nel tempo. Le serie storiche vengono studiate sia per interpretare un fenomeno, individuando componenti di trend, di ciclicità, di stagionalità e/o di accidentalità, sia per prevedere il suo andamento futuro.

In generale, per serie si intende la classificazione di diverse osservazioni di un fenomeno rispetto ad un carattere qualitativo. Se tale carattere è il tempo, la serie viene detta storica o temporale.
Il fenomeno osservato, detto variabile, può essere osservato in dati istanti di tempo (variabile di stato: numero dei dipendenti di un'azienda, quotazione di chiusura di un titolo negoziato in borsa, livello di un tasso di interesse ecc.) o alla fine di periodi di lunghezza definita (variabili di flusso: vendite annuali di un'azienda, PIL trimestrale ecc.).
Indicando con Y il fenomeno, si indica con Y_t un'osservazione al tempo t, potendo t variare da 1 a T, dove T è il numero complessivo degli intervalli o dei periodi temporali considerati.
In generale una serie storica è così definita y_t={y₁,y₂,y₃,....,y_T};la serie storica avrà dimensione T.

Trasformazione di Box-Muller

È un metodo per generare coppie di numeri casuali indipendenti e distribuiti gaussianamente con media nulla e varianza uno.

La trasformazione viene comunemente espressa in due forme. La forma principale è quella del lavoro originale: si campionano due numeri dalla distribuzione uniforme sull'intervallo  e si ricavano due numeri distribuiti normalmente. La forma polare campiona due numeri su un intervallo differente () e permette di ricavare due numeri distribuiti normalmente senza l'uso delle funzioni seno e coseno.

FORMA BASE 

Siano  e 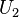 due variabili aleatorie indipendenti ed uniformemente distribuite nell'intervallo . Sia

  

e

Allora Z₀ e Z₁ sono variabili aleatorie indipendenti con distribuzione normale di deviazione standard unitaria.

La dimostrazione è basata sul fatto che, in un sistema cartesiano bidimensionale nel quale le coordinate X e Y sono descritte da due variabili casuali indipendenti normalmente distribuite, le variabili casuali R² e  nelle corrispondenti coordinate polari sono a loro volta indipendenti e possono essere espresse come  e